We may receive a commission when you use our affiliate links. However, this does not impact our recommendations.
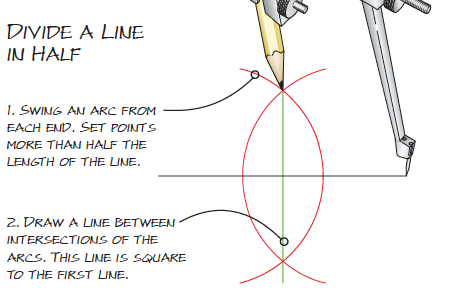
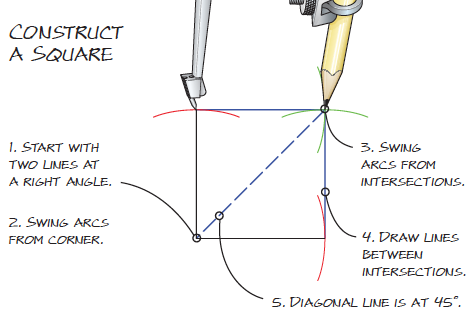
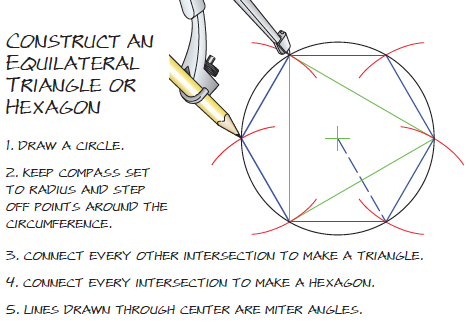
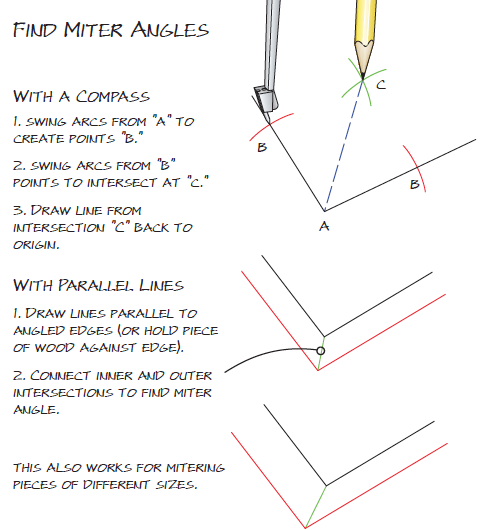
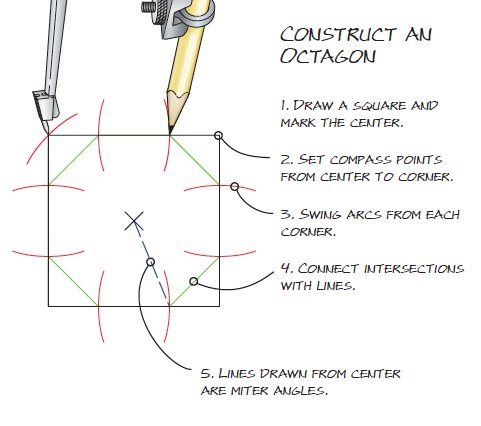
Many layout problems that seem to call for math can be quickly solved with a compass and a straightedge. Numbers can confuse and complicate the situation. What you need to know is how to make things fit –
not necessarily what numbers describe the lines and angles. Here are a few time-tested methods.
– Robert W. Lang; illustrations by Mary Jane Favorite
You may also be interested in “Essential Guide to the Steel Square” by Ken Horner.
